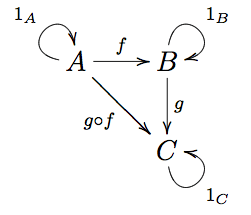
-
Collection of objects (e.g. A, B, C, …)
-
Collection of arrows (morphisms) between the objects (f : A → B, g : B → C)
-
Composition of arrows (e.g. h = g o f : A → C)
Under the following rules:
-
f o (g o h) = (f o g) o h
(The composition of morphisms needs to be associative)
-
f o idA = f = idB o f
(The identity morphism/Unit)
Where idX is the identity function (idX : X → X) so that idX(x) = x, where x ∈ X.
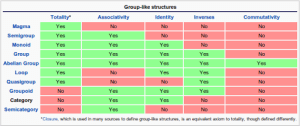
Here is a list of other group-like structures and their properties:
bor0's reflective blog 