I had some fun time reading http://onlinestatbook.com/2/regression/intro.html today. It includes formulas for calculating linear regression of a data set.
Linear regression is used for predicting a value of a variable from a list of known values.
For example if a and b are related variables, then linear regression can predict the value of the one given the value for the other.
Here’s an implementation in Racket:
#lang racket
(require plot)
(define (sum l) (apply + l))
(define (average l) (/ (sum l) (length l)))
(define (square x) (* x x))
(define (variance l)
(let ((avg (average l)))
(/
(sum (map (lambda (x) (square (- x avg))) l))
(- (length l) 1))))
(define (standard-deviation l) (sqrt (variance l)))
(define (correlation l)
(letrec
((X (map car l))
(Y (map cadr l))
(avgX (average X))
(avgY (average Y))
(x (map (lambda (x) (- x avgX)) X))
(y (map (lambda (y) (- y avgY)) Y))
(xy (map (lambda (x) (apply * x)) (map list x y)))
(x-squared (map square x))
(y-squared (map square y)))
(/ (sum xy) (sqrt (* (sum x-squared) (sum y-squared))))))
(define (linear-regression l)
(letrec
((X (map car l))
(Y (map cadr l))
(avgX (average X))
(avgY (average Y))
(sX (standard-deviation X))
(sY (standard-deviation Y))
(r (correlation l))
(b (* r (/ sY sX)))
(A (- avgY (* b avgX))))
(lambda (x) (+ (* x b) A))))
(define (plot-points-and-linear-regression the-points)
(plot (list
(points the-points #:color 'red)
(function (linear-regression the-points) 0 10 #:label "y = linear-regression(x)"))))
So, for example if we call it with this data set:
(define the-points '(
( 1.00 1.00 )
( 2.00 2.00 )
( 3.00 1.30 )
( 4.00 3.75 )
( 5.00 2.25 )))
(plot-points-and-linear-regression the-points)
This is the graph that we get:
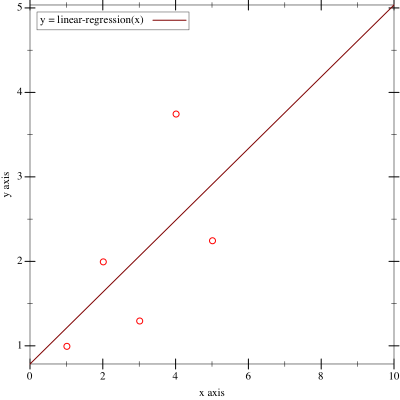
Cool, right?
One thought on “Predicting values with linear regression”