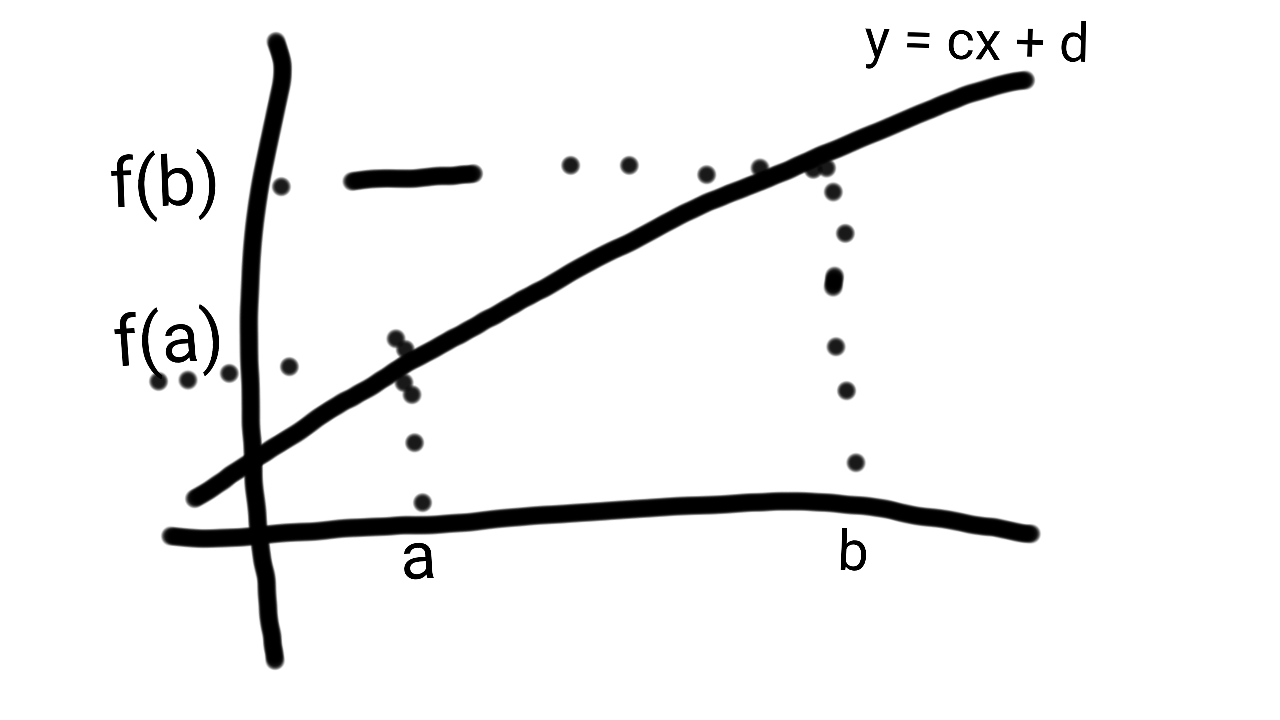
Deriving point-slope from slope-intercept form

In this post we’ll derive the form of a linear equation between two points by simply knowing one thing:

Given $y = cx + d$ , this line passes through the point $A = (x, y)$ .

The inspiration of this post is deriving the derivative.

So, let’s get started. We want to find an equation of a line that passes through $A = (a, f(a)), B = (b, f(b))$ .

So we plug the points into the equation of a line to obtain the system:

$\begin{cases} f(a) = ma + d \\ f(b) = mb + d \end{cases}$

Solving for m, d:

$\begin{cases} f(a) - ma = d \\ (f(b) - f(a))/(b - a) = m \end{cases}$

To eventually conclude $y - f(a) = m(x - a)$ .

In some of the next posts, we will derive the formula of a derivative of a function.

Published by Boro Sitnikovski