Definition of the mathematical limit

This post assumes knowledge in mathematical logic and algebra.
We will stick to sequences for simplicity, but the same reasoning can be extended to functions. For sequences we have one direction: infinity.

Informally, to take the limit of something as it approaches infinity is to determine its eventual value at infinity (even though it may not ever reach it).

As an example, consider the sequence $a_n = \frac {1} {n}$ . The first few elements are: 1, 0.5, 0.(3), 0.25, and so on.

Note that $\frac {1} {\infty}$ is undefined as infinity is not a real number. So here come limits to the rescue.

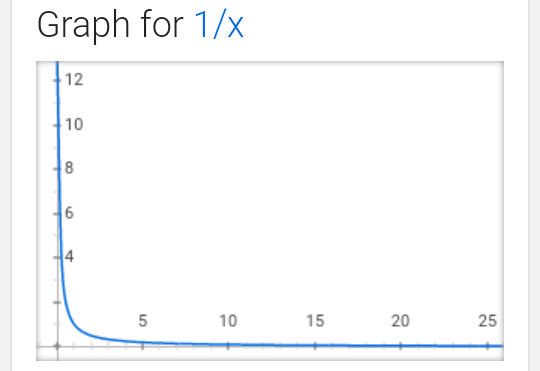
If we look at its graph, it might look something like this:

We can clearly see a trend that as x -> infinity, 1/x tries to “touch” the horizontal axis, i.e. is equal to 0. We write this as such: $\lim_{n \to \infty} \frac {1} {n} = 0$ .

Formally, to say that $\lim_{n \to \infty} a_n = a$ , we denote: $(\forall \epsilon > 0) (\exists N \in \mathbb {N}) (\forall n \geq N) (|a_n - a| < \epsilon)$ . Woot.

It looks scary but it’s actually quite simple. Epsilon is a range, N is usually a member that starts to belong in that range, and the absolute value part says that all values after that N belong in this range.

So for all ranges we can find a number such that all elements after that number belong in this range.

Why does this definition work? It’s because when the range is too small, all elements after N belong in it, i.e. the values of the sequence converge to it endlessly.

As an example, let’s prove that $\lim_{n \to \infty} \frac {1} {n} = 0$ . All we need to do is find a way to determine N w.r.t. Epsilon and we are done.

Suppose Epsilon is arbitrary. Let’s try to pick N s.t. $N = \frac {1} {\epsilon}$ .

Let’s see how it looks for $\epsilon = \frac {1} {2}$ : for $n > \frac {1} {\epsilon} = 2$ , we have: $a_n < \epsilon$ . This is obviously true since $1/4 < 1/3 < 1/2$ . So there’s our proof.