CoC base terms – Type and Prop – bor0's reflective blog

In mathematics, a judgement is a logical statement in the meta language
An inference rule means that for a given list of judgements $J_1, J_2, \ldots, J_n$ , we can infer that $J$ , which we denote as $\frac{J_1, J_2, \ldots, J_N}{J}$
Calculus of Constructions is a type theory based on intuitionistic logic.

If 1 and 2 don’t make much sense, I found this picture on Twitter to be useful:

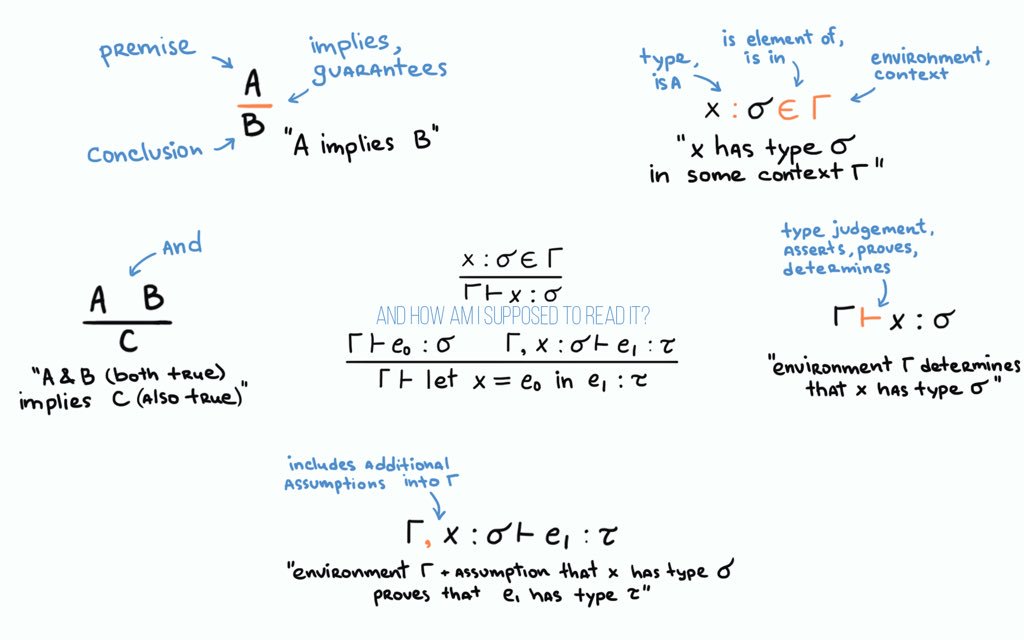
For $K$ being either $\text{Type}$ or $\text{Prop}$ , Calculus of Constructions has the following inference rule:

${\Gamma \ \vdash A \ : \ K \over {\Gamma, \ x:A \ \vdash \ x:A}}$

What this rule means is that $x$ can only be of type $A$ , if $A$ is of type $\text{Type}$ , or $A$ is of type $\text{Prop}$ .

The questions that I had were:

What are the (dis)advantages of limiting $A$ to be $K$ ?
Alternatively, what are the (dis)advantages of allowing infinite subtyping (allowing terms to be used as types)?
Why do we have these base types $\text{Type}$ and $\text{Prop}$ ?

First of all, we can already “emulate” something like “infinite subtyping” in Coq. For example, to “construct” foo : 3 : Nat : Type we can implement F : nat -> Type, then we have that F 3 : Type. Further, we can implement F' : F 3 -> Type, so F' foo is possible. It’s still of type Type but it kinda works.

But, what happens if we lift this restriction? Well that’s not an easy thing to do. At the very least we need some kind of well-formedness condition in place of $A : K$ , otherwise we can get judgements like $x : (\text{true} + 0) \ \vdash \ x : (\text{true} + 0)$ . So plainly lifting that restriction not only allows arbitrary terms that are not types, it even allows ill-typed terms which do not type-check.

So foo : 3 : Nat : Type kind of makes no sense. To the left, we have the values we actually compute on; types classify those, and can in turn be classified. In other words, a : b means that a is an element of the “collection” b, but some of these elements are not collections.

So the reason why we have types/values distinction is computation and we can’t really bring them at the “same” level, even though dependent types try to blur the line between the two. We can have values in types, and types in values, but there’s still a difference.

This is why that judgement rule is so important 🙂

As usual, somebody had already considered this 🙂 I started a discussion on #coq@freenode and ##dependent@freenode and got some great answers. Thanks to pgiarrusso, lyxia, and mietek.