Meet them all

Here’s a funny algorithm task I was thinking about during lunch at Automattic Grand Meetup.

Given infinite tables and 900 people – they have lunch, then dinner, then lunch, etc. repeatedly. They can’t have lunch after lunch, or dinner after dinner. A lunch table consists of 8 persons and a dinner table consists of 4.

What is the least number (or a good lower bound) of lunches and dinners they need to have for every person to have met all other persons?

The trickiest bit about solving this problem is to construct the “best” lunch/dining table. By best I mean that the number of connections between each node in that graph (table) is minimum, and this should be valid for every table constructed in a single session.

Essentially, we’re trying to minimize $\sum _{p\in T}\deg(p)$ for every table such that all tables use the best permutation. In other words, we’re looking for a $T$ such that $\min \sum_{t \in T} \sum _{p\in t}\deg(p)$ where $t$ is a table (set of persons), $T$ is a set of tables and $p$ is a person.

To do this correctly (I believe) means to go through all permutations and find the best one. This means that we’re dealing with the complexity of at least $O(n!)$ (which is what it takes to build permutations).

Alternatively, another “acceptable” solution is making our algorithm greedy. We will see that even this may produce slow results, but we can still come up with a good (probably not best) lower bound.

Why is the greedy solution not as good as going through all permutations? Simply because it means that if a person we added to a table A (greedily) was instead added to table B, it would’ve produced much better results.

In any case, the algorithm to greedily construct such a table is:

Initially, the assigned persons to a table $t$ is an empty list
Pick a person $p$ (that hasn’t met all other persons) such that the intersection with the lists $t$ and “persons that $p$ met” is minimum*, and set $t := t + [p]$
Repeat 2 until the particular table is full
The new table is constructed, repeat 1 until all persons are assigned. Persons that have met all other persons can be discarded from the list

(* Note that this may not always be zero, for example, when a person has met all other persons except one, they may have to be put on a table such that other persons have already met others)

An implementation of this algorithm can be found here.

When I tried to run this algorithm against the number of Automatticians (which is around 900), it took some time. In fact, I waited a few minutes then decided to stop it. To give a brief sense, here’s how long it took to calculate for 300 persons (on my powerful MacBook):

$ time php best_lunches.php 300
99

real	3m13.802s
user	3m11.210s
sys	0m1.025s

It gets very slow even for small numbers. It was fast for numbers from 0 to 100 though, so maybe we can do something else? Here’s the data set it produced:

[ (0, 1), (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 3), (9, 3), (10, 5), (11, 5), (12, 5), (13, 5), (14, 5), (15, 4), (16, 7), (17, 7), (18, 7), (19, 7), (20, 7), (21, 8), (22, 9), (23, 9), (24, 9), (25, 9), (26, 10), (27, 10), (28, 11), (29, 11), (30, 10), (31, 8), (32, 12), (33, 13), (34, 13), (35, 13), (36, 13), (37, 14), (38, 13), (39, 13), (40, 14), (41, 15), (42, 15), (43, 16), (44, 15), (45, 16), (46, 15), (47, 16), (48, 16), (49, 17), (50, 16), (51, 17), (52, 17), (53, 18), (54, 17), (55, 18), (56, 18), (57, 19), (58, 19), (59, 19), (60, 20), (61, 20), (62, 19), (63, 15), (64, 23), (65, 23), (66, 24), (67, 25), (68, 25), (69, 25), (70, 25), (71, 25), (72, 25), (73, 27), (74, 27), (75, 27), (76, 27), (77, 28), (78, 28), (79, 29), (80, 28), (81, 29), (82, 29), (83, 29), (84, 29), (85, 29), (86, 29), (87, 29), (88, 29), (89, 29), (90, 29), (91, 29), (92, 30), (93, 30), (94, 31), (95, 31), (96, 31), (97, 31), (98, 31), (99, 32), (100, 31) ]

If we graph that data set we’ll notice it almost follows a linear trend. Let’s do that and produce a linear regression:

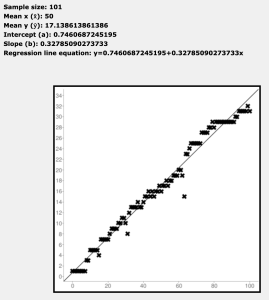
It’s not bad: if we input 300 to that linear equation we’ll get ~99.10 where the program produced 99. As another example, for 200 we get ~66.31 where the program produced 63. Inputting 900 (which is what we initially wanted) produces a number ~295.81.

We may have not solved it fully, but we have a good idea 🙂