I was looking at Wikipedia’s article regarding Monoids, and decided that it was interesting to make a post regarding the section “Monoids in Computer Science” http://en.wikipedia.org/wiki/Monoid#Monoids_in_computer_science.

So there they have posted this formula: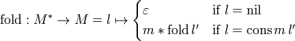

And let’s also take a look at Haskell’s definition for fold:

(>>>) = (++) 

fold []     = []
fold (m:l') = m >>> (fold l')

Notice the relation between the formulas? Just replace >>> with *, and there you have it!

Regarding the types, in Haskell we have:

*Main> :t fold
fold :: [[a]] -> [a]

And in Mathematics, we have:
fold: M* -> M

The star here represents Kleene’s star, and it is defined to be all concatenations on the elements of the set M, including the empty string (). Example, if M = {a, b} then M* = {(), (a), (b), (a,a), (a,b), (b,b), (b,a), (a,b,a), …}. So what this means is, that if we have M defined as list of integers, then M* would be list of list of integers (which is the result of list concatenation of the elements of M).

And what is fold? Well, fold basically takes a Monoid and applies its operation. Now that we have these two formulas, we can show how fold operates on a Monoid.

Let’s consider the Monoid M ([Int], ++, []). First, to prove that this triple makes a monoid, we must first take a look at the definition of ++:

[]     ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys) (*)

1. Closure
Namely, the (++) is the list concatenation operator, and when we concatenate two lists, we get list as an output, according to ++ definition.

2. Associativity
(xs ++ ys) ++ zs = xs ++ (ys ++ zs), order of evaluation will not change the resulting list
To prove this, we again need to look at ++ definition.

We can use Structural Induction in order to prove associativity.

Base case: If we let x = ys + zs, then [] ++ x = x by definition, LHS equals to x. and for the RHS, we get “” + ys = ys by definition, so ys ++ zs == x, and so LHS = RHS.

Inductive step: Assume that (xs ++ ys) ++ zs = xs ++ (ys ++ zs)

We need to prove that ((x:xs) ++ ys) ++ zs = (x:xs) ++ (ys ++ zs)

LHS: by (*) = (x : (xs ++ ys)) ++ zs => let xs ++ ys = p => x : p ++ zs = x : ((xs ++ ys) ++ zs)
RHS: by (*) = x : (xs ++ (ys ++ zs)) => by assumption => x : ((xs ++ ys) ++ zs)

So we get that LHS = RHS.

3. Identity
The empty list [] is the identity here, because [] ++ ys or ys ++ [] always equals to ys, according to ++ definition (already proved by base case in 2).

Now, we can start playing around with our fold:

*Main> fold [[1,2], [3]] -- per Monoid M
[1,2,3]
*Main> fold [['a'],['b'],['c']] -- same as Monoid M, but operates on set [Char] instead of [Int]
"abc"

I was playing around today with attempting to re-define the definition of Haskell’s list. The list in Haskell is well defined using the symbols [ and ], and some additional operators such as : and ++

For example, if we have a list [1, 2, 3] we can easily append a number to the beginning (prefix) by doing 0:[1, 2, 3], or we can append a number to the end (postfix) by doing [1, 2, 3] ++ [4].

The difference between these two operations is that the former only takes constant time, since it is appending a value to the beginning of the list, while the latter takes O(n) time, because it first needs to traverse the list and then append another list ([value]) to the end of it.

So anyway, back to playing with recursive definitions. My definition of the list was:

data List a = Nil | Cons a (List a) deriving (Show)

What this says is that the type List can have 2 constructors, either Nil or Cons. If it’s Nil, then it’s Nil (end of list), however, if it’s Cons, then we can add a value to it (e.g. Cons 3), but after Cons we must also add another “List a” type (which can be either Nil or another recursive Cons).

So this recursive definition allows us to define a list. And this is how lists are basically implemented in LISP. For example, if we wanted to represent [1, 2, 3] using our Cons Nil representation, we would have something like:

Cons 1 (Cons 2 (Cons 3 Nil))

You can play around with it as much as you like; what I did was only implement the ++ operator:

add' :: List a -> List a -> List a
add' Nil ys = ys
add' (Cons x xs) ys = Cons x (add' xs ys)

Example usage:

*Main> add' (Cons 1 (Cons 2 (Cons 3 Nil))) (Cons 4 Nil)
Cons 1 (Cons 2 (Cons 3 (Cons 4 Nil)))

When we speak of recursion for Haskell, we can define fix point like this:

Prelude> let fix f = f (fix f)
Prelude> :t fix
fix :: (t -> t) -> t

We can see from its type that it is well defined, i.e. the argument should be a function that takes a t and returns a t.

So now consider we have factorial defined as:
Prelude> let fact n = if n == 0 then 1 else n * fact(n-1)

So we can use it like:
Prelude> (fix (\x -> fact)) 4
24

This is great!

So, regarding lambda calculus, recursion is defined as:
Y := λg.(λx.g (x x)) (λx.g (x x))

But, if we tried to do that in Haskell, we’d get something like:

Prelude> \g -> (\x -> g (x x)) (\x -> g (x x))
:2:35:
    Occurs check: cannot construct the infinite type: t1 = t1 -> t0
    In the first argument of `x', namely `x'
    In the first argument of `g', namely `(x x)'
    In the expression: g (x x)

So this is Haskell warning us about infinite types. And why does that recursion definition work with lambda calculus?

Well, the reason is that lambda calculus is untyped (unless we are talking about typed lambda calculus, which we aren’t :-)), and Haskell is typed.

So in the world of typed languages, that lambda expression is not possible.
Consider x :: a -> a for some choice of a. To apply x to something, that something must have type a. So, to apply to x, x :: a. But that means a == a->a.

But hey, we still have fixed point combinators!