Meet them all

Here’s a funny algorithm task I was thinking about during lunch at Automattic Grand Meetup.

Given infinite tables and 900 people – they have lunch, then dinner, then lunch, etc. repeatedly. They can’t have lunch after lunch, or dinner after dinner. A lunch table consists of 8 persons and a dinner table consists of 4.

What is the least number (or a good lower bound) of lunches and dinners they need to have for every person to have met all other persons?

Continue reading “Meet them all” →

Abstraction and generalization of objects

Abstraction is the process of removing details of objects. We step back from concrete objects to consider a number of objects with identical properties. So a concrete object can be looked at as a “superset” of a more abstract object.

A generalization, then, is the formulation of general concepts from specific instances by abstracting common properties. A concrete object can be looked at as a “subset” of a more generalized object.

Continue reading “Abstraction and generalization of objects” →

Arithmetic on Algebraic Data Types

Per Wikipedia, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types.

Haskell’s algebraic data types are named such since they correspond to an initial algebra in category theory, giving us some laws, some operations and some symbols to manipulate. — Don Stewart

The operations being:

  • Sum type = + (data Either a b = Left a | Right b)
  • Product type = * (data Product a b = Product a b)
  • Function type = ^ (The -> kind in Haskell)

Continue reading “Arithmetic on Algebraic Data Types” →

Brief introduction to Machine Learning with Gradient Descent

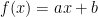In Mathematics, there are many curves. From a constant curve f(x) = b, to a linear one f(x) = ax + b, to a quadratic one f(x) = ax^2 + bx = c to …, you name it.

Now, imagine that there is a huge data set with some points (think ordered pairs for simplicity), but not all points are defined. Essentially, machine learning is all about coming up with a curve (based on a chosen model) by filling gaps.

Once we agree on the model we want to use (curve we want to represent), we start with some basic equation and then tweak its parameters until it perfectly matches the data set points. This process of tweaking (optimization) is called “learning”. To optimize, we associate a cost function (the error or delta between the values produced by the equation and the data set) and we need to find for which parameters this cost is minimal.

Gradient descent is one algorithm for finding the minimum of a function, and as such it represents the “learning” part in machine learning. I found this video by StatQuest, along with this video by 3Blue1Brown to be super simple explaining these concepts, and naturally, this article will be mostly based on them.

In this article I will assume some basic set theory, and also derivatives. Further, through example, we will:

  1. Define what the curve (model) should be
  2. Come up with a data set
  3. Do the “learning” using gradient descent
Continue reading “Brief introduction to Machine Learning with Gradient Descent” →