1. Collection of objects (e.g. A, B, C, …)

2. Collection of arrows (morphisms) between the objects (f : A → B, g : B → C)

3. Composition of arrows (e.g. h = g o f : A → C)

1. f o (g o h) = (f o g) o h
   (The composition of morphisms needs to be associative)

2. f o id_A = f = id_B o f
   (The identity morphism/Unit)

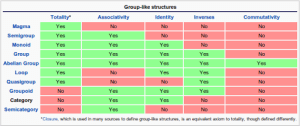
A monoid is an (abstract) algebraic structure. Monoids (and other algebraic structures in general) are useful because they share some set of properties, which then programmers can take for granted.

Let’s give a mathematical definition of what monoids represent, and then we will show some examples.

So, a monoid is basically consisted of a set S, along with a binary operation • (note: this doesn’t have to mean multiplication specifically, it can be any operation), so that the following properties are fulfilled:

1. Closure
(∀a,b ∈ S): a•b ∈ S
This basically means that the operation • belongs in the same set as the arguments a and b.

2. Associativity
(∀a,b,c ∈ S): (a•b)•c = a•(b•c)
This means that the order of evaluating expressions will not matter.

3. Identity
(∃e∀a): a•e = e•a = a

For example, the set of natural numbers ℕ together with the binary operation + (standard addition) make up a monoid. Let’s see how:

1. Closure – Every addition of two natural numbers is also a natural number.
2. Associativity – Order of addition will not change the result, i.e. (a+b)+c = a+(b+c)
3. Identity – The identity element of this specific monoid is e=0, because we have that any natural number added to 0, or 0 added to any natural number will be the natural number itself.

Structural induction is a generalization of mathematical induction.

To see how, consider the definition of naturals (which mathematical induction is based on):

Inductive nat : Set :=
  | O => nat
  | S => nat -> nat.

So, generally what we do is prove the base case , and then prove the recursive step by assuming .

Structural induction can be applied more generally, say lists.

Inductive natlist : Set :=
  | nil  => natlist
  | cons => nat -> natlist -> natlist.

In this case we prove the base case , and then prove the recursive step by assuming , where .

So as an example, let’s try to prove that .

First, let’s look at the definitions for map and id:

map _ []     = []
map f (x:xs) = f x : map f xs
id x         = x

We use induction on x.

Base case:

Inductive step: Assume that , and prove that .

.

Eta-reduction: .

Q.E.D.

Here is a tiny proof, when doing primality test, why it is enough to check divisors only up to sqrt(n) instead of n:

Let n divide q.

If n < sqrt(q) < q
then n < sqrt(q) < q/n < q

q/n < q is trivial

sqrt(q) < q/n
1/sqrt(q) < 1/n

sqrt(q) > n

Alternatively

If sqrt(q) < n < q
then q/n < sqrt(q) < n < q

sqrt(q) < n
sqrt(q) > q/n

Implementation of the algorithm in Haskell:

primetest :: Int -> Bool
primetest x = primetest' x $ (ceiling.sqrt.fromIntegral) x
  where
  primetest' 1 _ = False
  primetest' x 1 = True
  primetest' x y = if x `mod` y == 0 then False else primetest' x (y - 1)

The part where I do (ceiling.sqrt.fromIntegral) may look magical, but what it does is:
1. Convert x from integer to something that sqrt accepts
2. Calculate the sqrt of it
3. Convert it back to integer