Recursive types in Haskell

I was playing around today with attempting to re-define the definition of Haskell’s list. The list in Haskell is well defined using the symbols [ and ], and some additional operators such as : and ++

For example, if we have a list [1, 2, 3] we can easily append a number to the beginning (prefix) by doing 0:[1, 2, 3], or we can append a number to the end (postfix) by doing [1, 2, 3] ++ [4].

The difference between these two operations is that the former only takes constant time, since it is appending a value to the beginning of the list, while the latter takes O(n) time, because it first needs to traverse the list and then append another list ([value]) to the end of it.

So anyway, back to playing with recursive definitions. My definition of the list was:

data List a = Nil | Cons a (List a) deriving (Show)

What this says is that the type List can have 2 constructors, either Nil or Cons. If it’s Nil, then it’s Nil (end of list), however, if it’s Cons, then we can add a value to it (e.g. Cons 3), but after Cons we must also add another “List a” type (which can be either Nil or another recursive Cons).

So this recursive definition allows us to define a list. And this is how lists are basically implemented in LISP. For example, if we wanted to represent [1, 2, 3] using our Cons Nil representation, we would have something like:

Cons 1 (Cons 2 (Cons 3 Nil))

You can play around with it as much as you like; what I did was only implement the ++ operator:

add' :: List a -> List a -> List a
add' Nil ys = ys
add' (Cons x xs) ys = Cons x (add' xs ys)

Example usage:

*Main> add' (Cons 1 (Cons 2 (Cons 3 Nil))) (Cons 4 Nil)
Cons 1 (Cons 2 (Cons 3 (Cons 4 Nil)))

Recursion in Haskell and LC

When we speak of recursion for Haskell, we can define fix point like this:

Prelude> let fix f = f (fix f) Prelude> :t fix fix :: (t -> t) -> t

We can see from its type that it is well defined, i.e. the argument should be a function that takes a t and returns a t.

So now consider we have factorial defined as:
Prelude> let fact n = if n == 0 then 1 else n * fact(n-1)

So we can use it like:
Prelude> (fix (\x -> fact)) 4 24

This is great!

So, regarding lambda calculus, recursion is defined as:
Y := λg.(λx.g (x x)) (λx.g (x x))

But, if we tried to do that in Haskell, we’d get something like:

Prelude> \g -> (\x -> g (x x)) (\x -> g (x x)) :2:35: Occurs check: cannot construct the infinite type: t1 = t1 -> t0 In the first argument of `x', namely `x' In the first argument of `g', namely `(x x)' In the expression: g (x x)

So this is Haskell warning us about infinite types. And why does that recursion definition work with lambda calculus?

Well, the reason is that lambda calculus is untyped (unless we are talking about typed lambda calculus, which we aren’t :-)), and Haskell is typed.

So in the world of typed languages, that lambda expression is not possible.
Consider x :: a -> a for some choice of a. To apply x to something, that something must have type a. So, to apply to x, x :: a. But that means a == a->a.

But hey, we still have fixed point combinators!

Lambda calculus

Lambda calculus is a theoretical programming language (with same expressive power as a Turing Machine). It is interesting because there is no state, and it consists only of two operators: . and λ.

If you want to learn more, visit the Wikipedia article http://en.wikipedia.org/wiki/Lambda_calculus as this will be only a short introduction.

So, since we have no state, we have no variables. We only have constants. Numbers are defined like:

1 := λf x. f x
2 := λf x. f (f x)

In other words, we can define 1 as f(x), and 2 as f(f(x)) (we get to define f and x ourselves).

Functions in lambda fall in two categories: abstraction and application.

Abstraction is when we define a function and apply no arguments to it.
Application is when we apply arguments to some abstraction (already defined function).

SUCC (successor) example:

SUCC is defined as

SUCC := λnfx. f (n f x)

So, doing SUCC 1 we get

(λnfx. f (n f x))(λf x. f x) =
λfx = f ((λf x. f x) f x) = f (f x) = 2

Desiderata

Go placidly amid the noise and haste, and remember what peace there may be in silence.
As far as possible without surrender be on good terms with all persons.
Speak your truth quietly and clearly; and listen to others, even the dull and ignorant; they too have their story.
Avoid loud and aggressive persons, they are vexations to the spirit.
If you compare yourself with others, you may become vain and bitter;
for always there will be greater and lesser persons than yourself.

Enjoy your achievements as well as your plans.
Keep interested in your career, however humble; it is a real possession in the changing fortunes of time.
Exercise caution in your business affairs; for the world is full of trickery.
But let this not blind you to what virtue there is; many persons strive for high ideals;
and everywhere life is full of heroism.

Be yourself.
Especially, do not feign affection.
Neither be critical about love; for in the face of all aridity and disenchantment it is as perennial as the grass.

Take kindly the counsel of the years, gracefully surrendering the things of youth.
Nurture strength of spirit to shield you in sudden misfortune. But do not distress yourself with imaginings.
Many fears are born of fatigue and loneliness. Beyond a wholesome discipline, be gentle with yourself.

You are a child of the universe, no less than the trees and the stars;
you have a right to be here.
And whether or not it is clear to you, no doubt the universe is unfolding as it should.

Therefore be at peace with God, whatever you conceive Him to be,
and whatever your labors and aspirations, in the noisy confusion of life keep peace with your soul.
With all its sham, drudgery and broken dreams, it is still a beautiful world. Be careful. Strive to be happy.

Fury Swipes Mechanics

I bet that you have heard this question a lot before,
What’s the best spell in DotA?

Now of course, this question makes you instantly think that the asker is a noob.
So you can’t really find an answer to that question, but the next question indeed has an answer:

What’s the best DMG spell in DotA?
Now, such spell really exists, and the best DMG spell (orb) is:

Fury Swipes
Roshan dead in 26 hits, level 7. No damage items, at ALL!

But of course you’ll say, “Bah, what’s this? Everybody knows Ursa is a very dangerous hero!”.
That’s true, but this article will show you why it really is such a great hero,
and will also show you the difference between normal attacks and Fury Swipes attacks.

Ursa Warrior attack

Before I start, please do not mix this with Necrolyte’s ultimate for instance.
That’s a powerful spell of course, but we will be discussing strictly about normal hits here..

Now begins the mathematics.
Please note that as we go through this documentation (or call it whatever you want),
I will ignore all armors which decrease your damage.

I’ll first define what average damage means. Consider you’re playing Mirana,
and your damage stats look like 20 – 50 + 73. Then the average damage is computed this way:
(20+50)/2 + 73 = 35 + 73 = 108.

Why is this so? Because your hero has a chance to output damage in the range (20, 50) plus the
bonus damage you receive from items (73 in this case).

The average (which is a measure of the “middle” of some data set) usually gives you the “final”
number after n output of damage, then divided by n. This means that, no matter if your damage is 2 to 4,
in the real long run it will just equal to (2+4)/2 = 3.

Late game Mirana

Now consider you’re in some game, 40th minute, you got all these imba
items which make your damage stats look something like this: 93 – 104 + 130. Computing the
average, it gives us 228.5 damage (but that’s in the long run, remember?).
Okay, 1 hit equals 228.5 damage, 2 hits equal 2 * 228.5 damage, and so on…
We get that n hits equal n * 228.5 damage (linear)

I will not define what a mathematical function means, you’ll have to go through your high
(or even basic) school books to understand this. So we have this function:

f(n) = n * 269, n = positive integer.

This function gives us the total damage after n hits. So consider you hit your enemy
30 times, and we calculate this using our function: f(30) = 30*269 = 8070 total damage.

Now, if you spent enough time in school, you’d instantly notice that this function
is a linear function. And it’s monotone increasing –
meaning that, the more hits we do, the more damage we do which is logical.

But now, enough examples, time to go back to Fury Swipes to see what’s it all about.
So the definition of this spell is pretty clear:
“Each attack deepends the wound in the target, causing each attack
to deal 25 more damage than the previous attack.”

Let a = average dmg, now we have:
I = a + 25 (This is the first attack, average dmg + 25 [Fury Swipes dmg])
II = I + 25 (This is the second attack, first attack + 25 [Fury Swipes dmg])
III = II + 25 (This is the third attack, second attack + 25 [Fury Swipes dmg])
… and so on. The train is long, believe me 🙂

Let’s simplify these equations a bit to see if we get something better
so we can make a function out of it.

I = a + 25
II = I + 25 = (a + 25) + 25
III = II + 25 = (a + 25) + 25 + 25

Now we have all three attacks (separate), but to get the total damage,
we sum all 3 equations and we get:

Total = I + II + III = a + 25 + (a + 25 + 25) + (a + 25 + 25 + 25)

So for three attacks, we have something like:
a + 1*25 + (a + 2*25) + (a + 3*25) = a + a + a + 25(1 + 2 + 3) = 3a + 25(Sum 0 to 3).

This sum (0 to n) given by the general formula n(n+1)/2 which is also learnt in high school.

So we have 3a + 25/2 3(3+1). Consider Ursa’s average dmg is 30,
we get total dmg done: 3 * 30 + 25/2 3*4 = 240 in just three hits! With only 30 dmg!

Now is the time to get into the general formula. As you proceed with expansion of
more and more hits, you will eventually get to this formula:

f(n) = na + 25/2 n(n+1) – where a = average damage, n = number of hits.

The special thing about this formula is that it’s quadratic!, and the others were just linear!
And what do we know about quadratic functions?
That they are much much bigger than the linear ones!

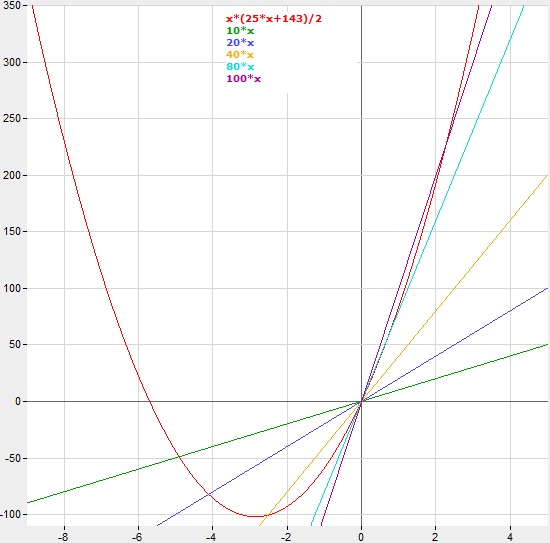
Difference between quadratic (red) and linear (green)

As x rises (our hits), the quadratic function (our total damage) rises faster!

The green graph shows the damage output of a hero with 10 average dmg (10x), the cyan graph shows the same
but for a 80 average dmg hero (80x).. and so on. The red graph is for Ursa’s Fury Swipes (with 59 avg. dmg).

If you have also heard of differentiation, there is a rule:
for f(x) = ax^n we have f'(x) = na*x^(n-1). Differentiation can show us the behaviour of a rise a function.
If you try to differentiate f(x) = ax, you will get f'(x) = a (normal hero).
But if you try to differentiate f(x) = ax^2 you get f'(x) = 2ax (Ursa Fury Swipes).
It is easy to notice that 2ax > a, so clearly x^2 rises faster than linear functions.

Roshan

Fury Swipes, as we all know, works against Roshan!

But what’s the big deal? How does it work? How many hits do we have to do in order to kill him?

Roshan starts with 7500 hp, and receives +500 hp bonus after every 5 minutes.
So the table looks something like this:

Start: 7500 hp
5th min: 8000 hp
10th min: 8500 hp
15th min: 9000 hp
20th min: 9500 hp
25th min: 10000 hp
30th min: 10500 hp
35th min: 11000 hp
40th min: 11500 hp
45th min: 12000 hp

Now, let’s calculate the average health of Roshan. This will give us a value that is only
between start and 45th min, because after that, Roshan’s HP does not increase,
it stays at 12000 constant.
(7500 + 8000 + 8500 + 9000 + 9500 + 10000 + 10500 + 11000 + 11500 + 12000)/10 = 9750

At level 7, you can max the bonus in Fury Swipes which is 25 damage,
and Ursa has 59 average damage with no damage items at all.
Let’s calculate the damage Ursa does in n hits: f(n) = 59*n + 25/2(n^2 + n) = n(25n + 143)/2

Let’s take a look at some values of this function:
f(22) = 7623 damage. (This is enough to kill Roshan with 7500 hp)
f(23) = 8257 damage. (Enough to kill Roshan with 8000 hp)
…
f(26) = 10309 damage. Enough to kill Roshan anywhere between start and 45th min.

But we will need more to kill him after 45 minutes have passed, or
f(29) = 12586 damage.
Roshan dead in 29 hits with no items at all at level 7?? Wow! Plus, we didn’t even count Enrage!
(Of course, you’d have to be able to handle the damage he deals)

Roshan

Enrage!

Now, let’s talk a bit about Enrage. Let’s first see how Enrage increases our damage.

Enrage

Level 1 is 4%, level 2 is 5%, and level 3 is 6%. Now, let’s make a formula out of this.
From previously, we had f(n) = na + 25/2 n(n+1) – where a = average damage, n = number of hits.

Now to expand this formula to calculate Enrage, we also need one more variable which will be our total health.
Also note that “Enrage doubles the damage dealt by Fury Swipes”. You can read at http://www.playdota.com/heroes/ursa-warrior.

With a little help from Cano from the PlayDotA forums, here is some info about Enrage:
1 damage is added to each attack (by triggers on the attack event), so we have n damage for n attacks;
the bonus damage from Enrage is 6*n*b/100, and then the Fury Swipes damage is dealt. This damage lacks 1 attack
so (n-1)*n*25/2 damage is dealt in n attacks. Now after we sum all this up, we get the next formula:

f(n) = n(a + 6/100b) + 25 n^2 + n – where a = average damage, b = current health, n = number of hits.

Please note that after Enrage effect passes, this formula does not work.
Also, your HP may drop in fights and it’s a bit hard to calculate the correct damage output. There are several
variables that come into play, such as: the damage that the enemy does to you (i.e. the rate of drop of your HP),
the time when you activated Enrage, etc. But I will not trouble you about this, since we already know that Ursa
deals a lot of damage with Fury Swipes alone.

Armor!

It’s Armor time!

From Blizzard’s official webpage:

For positive Armor, damage reduction =((armor)*0.06)/(1+0.06*(armor))
For negative Armor, it is damage increase = 2-0.94^(-armor) since you take more damage for negative armor scores.

Once you calculate these numbers, just multiply the damage reduction/increase by f(n).
That will give you the damage reduction/increase. Let p = damage reduction/increase. We have 2 cases:

1) If it’s reduction, you have total damage = f(n) – f(n)*p
2) If it’s increase, you have total damage = f(n) + f(n)*p

If you have read the whole tutorial, I thank you for your time! I had much fun writing this,
so I hope that you enjoyed the reading as I did enjoy the writing. Good luck!